Introduction
It is well-known now that the paradigm of escape from a potential well and the topology of phase space structures that mediate such escape are used in a broad array of problems such as isomerization of molecular clusters [1], reaction rates in chemical physics [2], [3], ionization of a hydrogen atom under electromagnetic field in atomic physics [4], transport of defects in solid state and semiconductor physics [5], buckling modes in structural mechanics [6], [7], ship motion and capsize [8], [9], [10], escape and recapture of comets and asteroids in celestial mechanics [11], [12], [13], and escape into inflation or re-collapse to singularity in cosmology [14]. As such a method that can identify the high dimensional phase space structures using low dimensional surface as probes can aid in quantifying the escape rates. These low dimensional surfaces has been shown to be of as reactive islands in chemical physics and lead to insights into sampling rare transition events [15], [16]. However, to benchmark the methodology, we first applied it to linear systems where the closed-form analytical expression of the phase space structures is known [17]. As the next step, in this chapter, we will focus on nonlinear Hamiltonian systems which have been extensively studied as "built by hand" models of galactic dynamics and for demonstrating quantum dynamical tunneling [18], [19], [20], [21], [22], [23], [24], [25], [26], [27]. The nonlinear Hamiltonian systems considered here have an underlying Hénon-Heiles type potential with the simplest form of nonlinearity, and show regular, quasi-periodic, and chaotic trajectories along with bifurcations of periodic orbits. A Hénon-Heiles type potential has a well with bottlenecks connecting the region of bounded motion (trapped region) to unbounded motion (escape off to infinity), and have rotational symmetry. In addition, these Hénon-Heiles type potentials are studied as first benchmark nonlinear systems in applying new phase space transport methods to astrophysical and molecular motion. In this chapter, we will present verification of a method that uses trajectory diagnostic on a low dimensional surface for revealing the phase space structures in 4 or more dimensions.
Conservative dynamics on an open potential well has received considerable attention because the phase space structures, normally hyperbolic invariant manifolds (NHIM) and its invariant manifolds, explain the intricate fractal structure of ionization rates [28], [29], [30]. Furthermore, the discrepancies in observed and predicted ionization rates in atomic systems has also been explained by accounting for the topology of the phase space structures. These have been connected with the breakdown of ergodic assumption that is the basis for using ionization and dissociation rate formulae [31]. This rich literature on chaotic escape of electrons from atoms sets a precedent for applying new methods for finding NHIM and its invariant manifolds in Hamiltonian with open potential wells [32], [30], [33], [34], [35].
As we noted earlier, trajectory diagnostic methods which can probe phase space to detect the high dimensional invariant manifolds have potential to be of use in many degrees-of-freedom models. One such method is the Lagrangian descriptors (LDs) that can reveal phase space structures by encoding geometric property of trajectories (such as, phase space arc length, configuration space distance or displacement, cumulative action or kinetic energy) initialised on a two dimensional surface (missing reference). The method was originally developed in the context of Lagrangian transport in time-dependent two dimensional fluid mechanics. However, it has also been successful in locating transition state trajectories in chemical reactions [36], [37], [38]. Besides, also being applicable to both Hamiltonian and non-Hamiltonian systems, as well as to systems with arbitrary time-dependence such as stochastic and dissipative forces, and geophysical data from satellite and numerical simulations [39], [40], [41], [42], [43].
The method of Lagrangian descriptors (LDs) is straightforward to implement computationally and it provides a "high resolution" method for exploring the influence of high dimensional phase space structure on trajectory behaviour. The method of LDs takes an opposite approach to that of classical Lyapunov exponent type calculations by emphasizing the initial conditions of trajectories, rather than their advected locations that is involved in calculating normalized rate of divergence. This is achieved by considering a two dimensional section of the full phase space and discretizing with a dense grid of initial conditions. Even though the trajectories wander off in the phase space, as the initial conditions evolve in time, there is no loss in resolution of the two dimensional section. In contrast to inferring the phase space structures from Poincaré sections, LD plots do not suffer from loss of resolution since the affects of the structure are encoded in the initial conditions and there is no need for the trajectory to return to the section. Our objective is to clarify the use of Lagrangian descriptors as a diagnostic on two dimensional sections of high dimensional phase space structures. This diagnostic is also meant to be used as the preliminary step in computing the NHIM, their stable and unstable manifolds using other computational means [44], [45], [46]. In this chapter, we will present the method's capability to detect the high dimensional phase space structures such as the NHIM, their stable, and unstable manifolds in the 2 DoF Barbanis system.
Barbanis 2 DoF Model
Model system: coupled harmonic 2 DoF Hamiltonian
As pointed out in the Introduction, our focus is to adopt a well-understood model system which is a 2 degrees-of-freedom coupled harmonic oscillator with the Hamiltonian
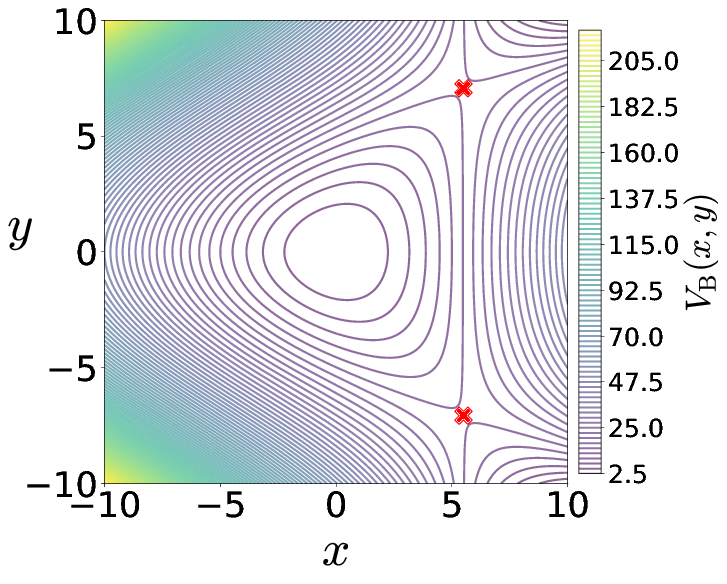
H(x,y,px,py)=T(px,py)+VB(x,y)=12p2x+12p2y+12ω2xx2+12ω2yy2+δxy2where ωx,ωy,δ are the harmonic oscillator frequencies of the x and y degree-of-freedom, and the coupling strength, respectively. We will fix the parameters as ωx=1.0,ωy=1.1,δ=−0.11 in this study. The two degrees-of-freedom potential is also referred to as Barbanis potential, and has been investigated as a model of galactic motion ([47], [18]), dynamical tunneling and molecular spectra in physical chemistry ([48], [49], [50]), structural mechanics and ship capsize ([9], [10]).
The equilibria of the Hamiltonian vector field are located at
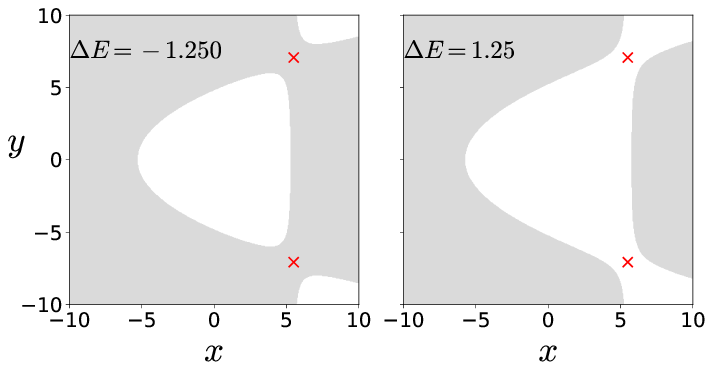
(−ω2y2δ,±1√2ωxωyδ,0,0)and(0,0,0,0)and are at total energy Ec=ω2xω4y8δ2 and 0 respectively. The energy of the two index-1 saddles (as defined and shown in App. 5.2.1) located at positive and negative y-coordinates and positive x-coordinate for δ<0 will be referred to as critical energy, Ec. In our discussion, we will refer to the total energy of a trajectory or initial condition in terms of the excess energy, ΔE=Ec−e, which can be negative or positive to denote energy below or above the critical energy. For the parameters used in this study, the index-1 saddle equilibrium points are located at (5.5,±7.071,0,0) and have energy, Ec=15.125.
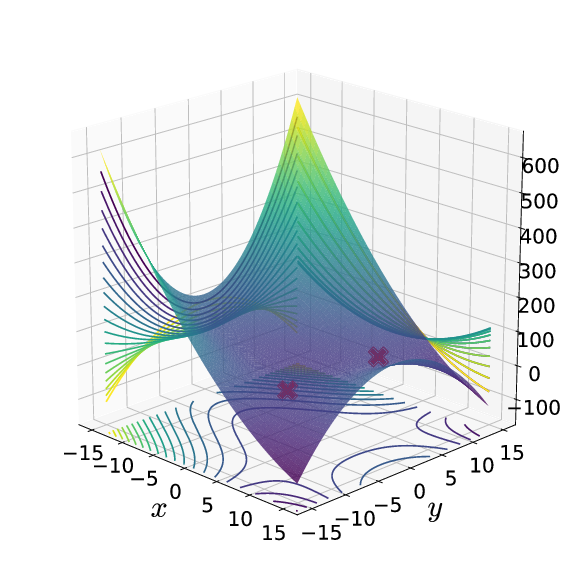
The contours of the coupled harmonic 2 DoF potential energy function in (???) is shown in Fig. fig:1 along with the 3D view of the surface. We note here that the potential has steep walls for x<0 when δ<0 and steep drop-off beyond the bottlenecks around the index-1 saddles. This leads to unphysical motion in the sense of trajectories approaching −∞ with ever increasing acceleration even for finite values of the configuration space coordinates [19].
In Fig. fig:2 we show the Hill's region, as defined in App. 5, for the model system (???). It is important to note here that even though Hill's region is shown on the configuration space, it captures the dynamical picture, that is the phase space perspective, of the Hamiltonian. This visualization of the energetically accessible and forbidden realm is the first step towards introducing two-dimensional surfaces to explore trajectory behavior. The complete description of the unstable periodic orbit and its invariant manifolds is described in App. 5.1 along with the visualization in the 3D space.
(SPLIT SET OF FIGURES INTO TWO, AS WELL AS CAPTIONS.)
Since this model system is conservative 2 DoF Hamiltonian, that is the phase space is R4, the energy surface is three dimensional, the dividing surface is two dimensional, and the normally hyperbolic invariant manifold (NHIM), referred to as the unstable periodic orbit, is one dimensional [51]. Now, if we consider the intersection of a two dimensional surface with the three-dimensional energy surface, we would obtain the one-dimensional energy boundary on the surface of section. We will focus our study by using the isoenergetic two-dimensional surface Uxpx,+={(x,y,px,py)|y=0,py(x,y,px;e)>0}
where the sign of the momentum coordinate enforces a directional crossing of the surface. Due to the form of the vector field (???) and choice of δ<0, this directionality condition implies motion towards positive y-coordinate.
In this article, detecting the phase space structures will constitute finding the intersection of the NHIM and its invariant manifolds with a two dimensional surface (for example, Eqn. (2)).
Results
We begin by noting that two-dimensional Poincaré surface of section have sufficient dimensionality to capture trajectories on a three dimensional energy surface, however for high dimensional systems trajectories can go "around" the two dimensional surface. One approach available in the literature is to use high dimensional Poincaré sections which can "catch" trajectories but are hard to visualize on paper or in the virtual 3D space. Even when gets around this issue, using suitable projective geometry, the fact that the qualitative analysis based on Poincaré sections depends on trajectories returning to this surface can not be circumvented since trajectories on and inside the spherical cylinders will not return to the Poincaré surface of section.
Coupled harmonic 2 DoF system
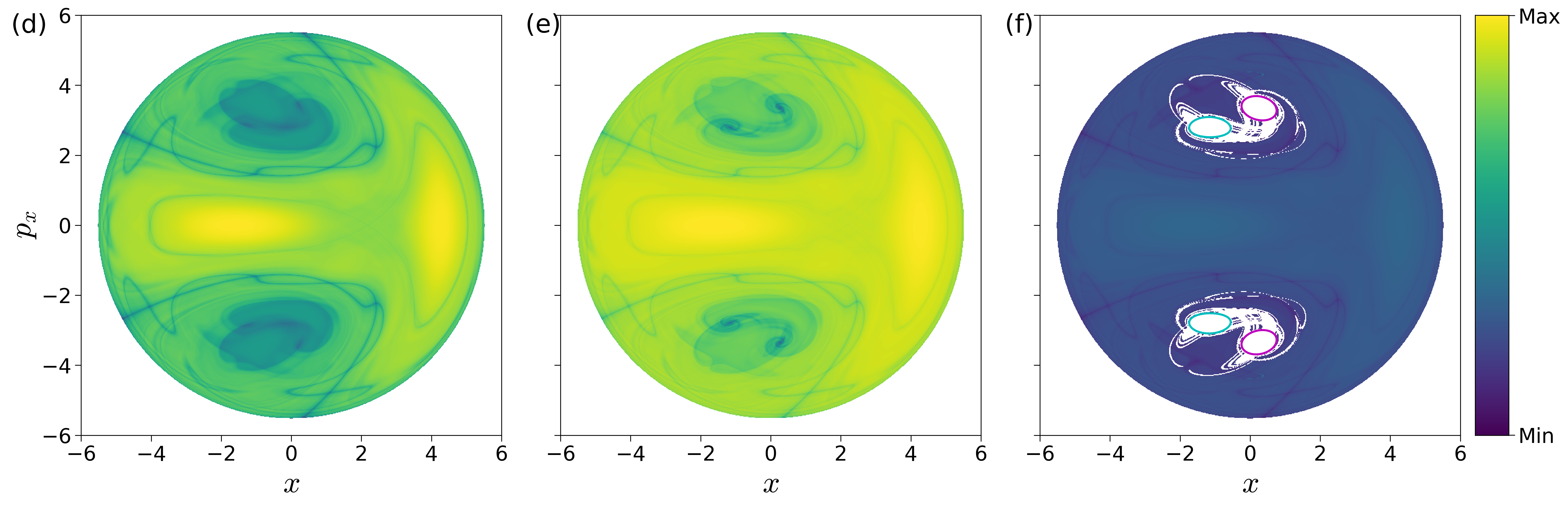
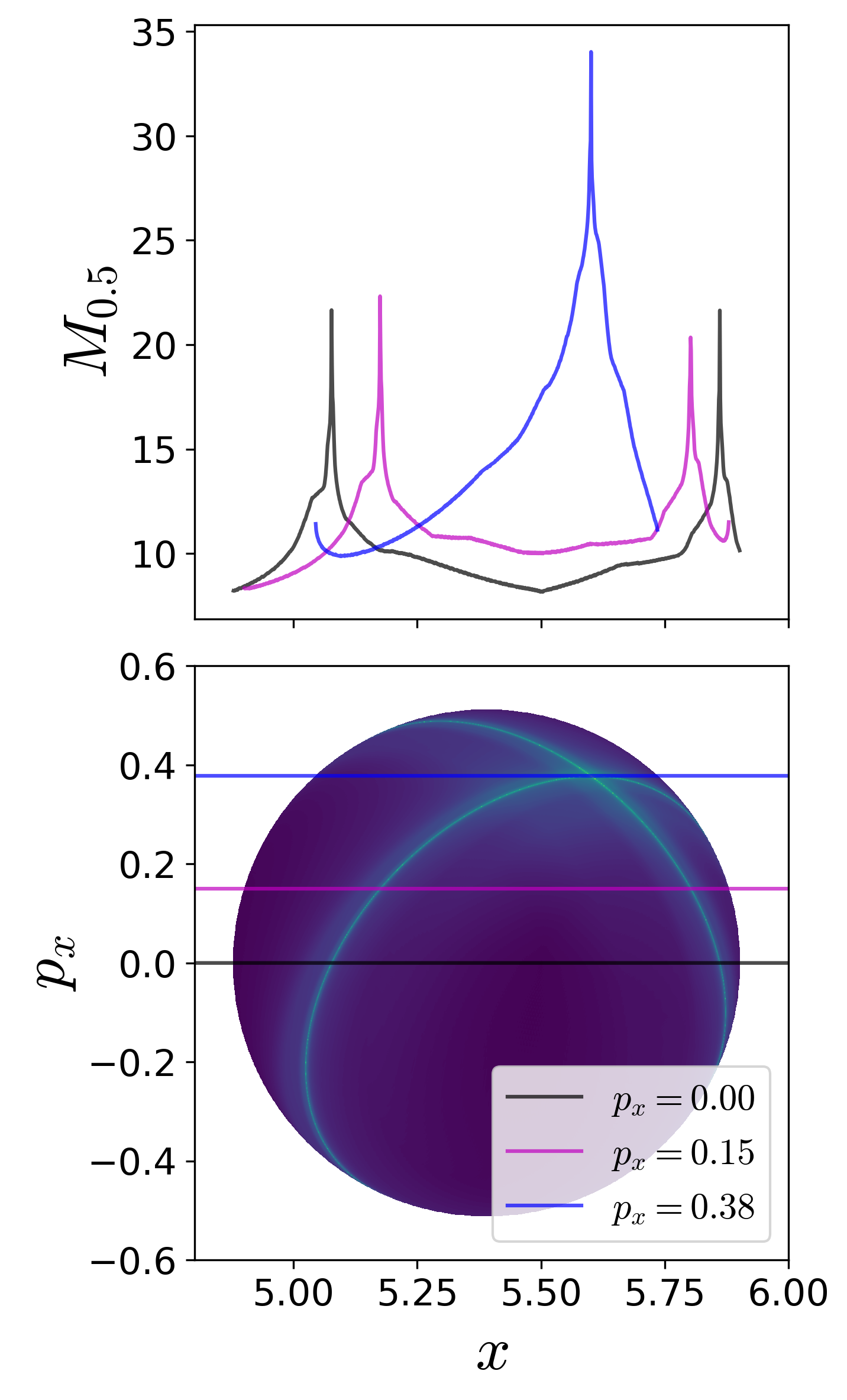
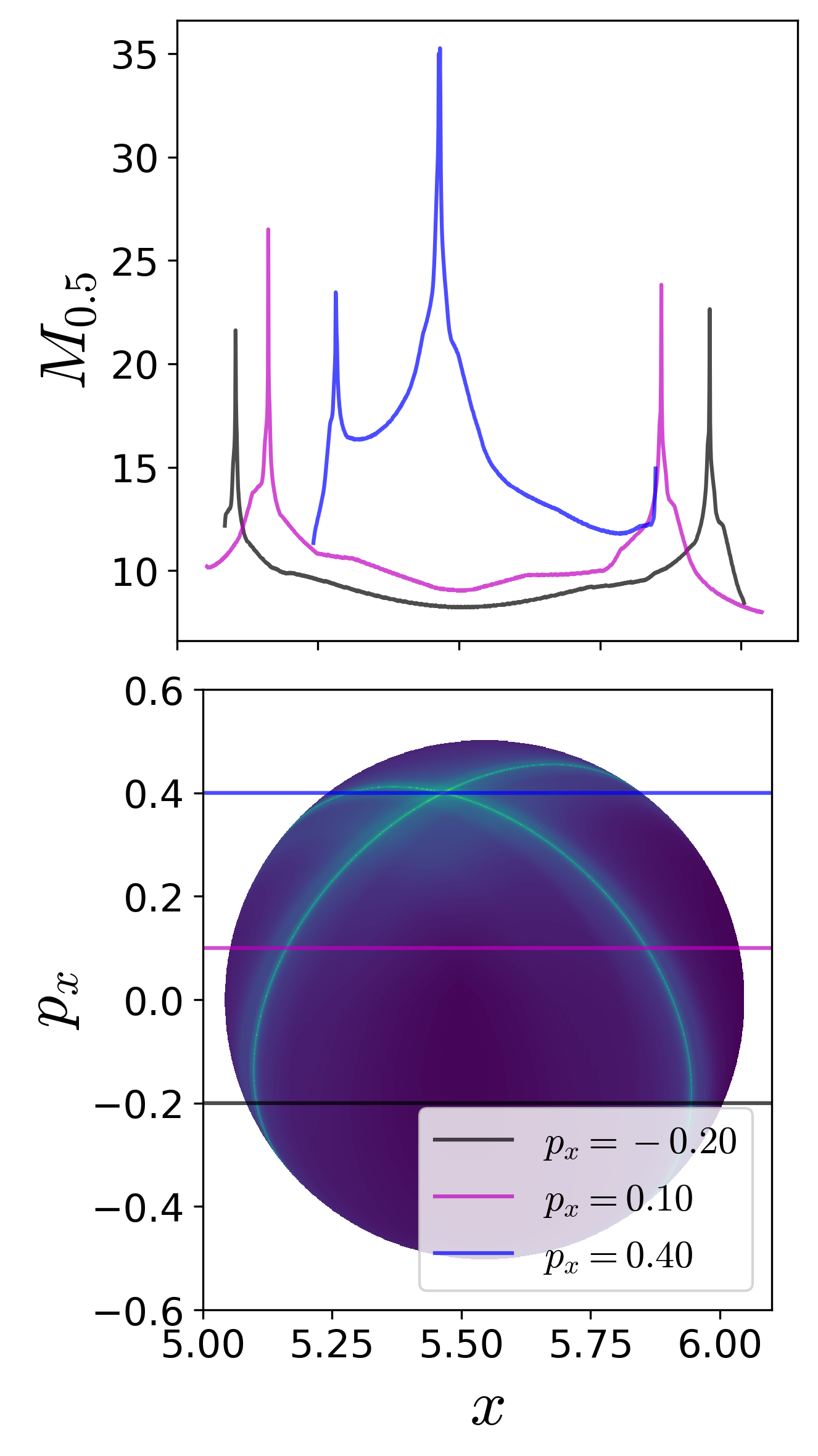
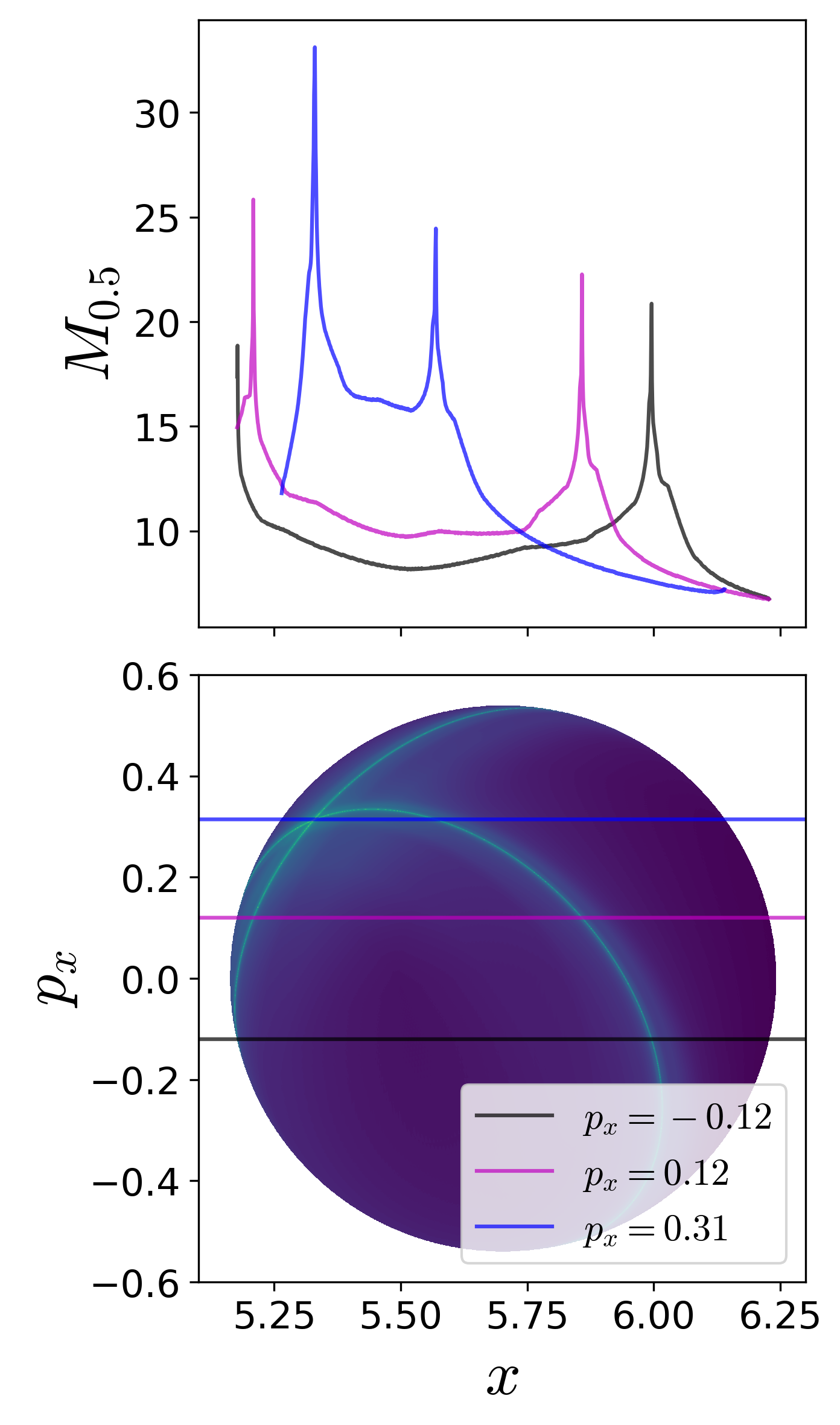
As discussed in aforementioned literature [52], [42], [53], points with minimum Lagrangian descriptor (LD) values and singularity are on the invariant manifolds. In addition, LD plots show dynamical correspondence with Poincaré sections (in the sense that regions with regular and chaotic dynamics are distinct in both Poincaré section and LD plots) while also depicting the geometry of manifold intersections [53], [42], [54]. This correspondence in the LD features and Poincaré section is confirmed in Fig. fig:3 where we show the Poincaré surface of section Eqn. (2) of trajectories and LD contour maps on the same isoenergetic two-dimensional surface for negative and positive excess energies. It can be seen that the chaotic dynamics as marked by the sea of points in Poincaré section is revealed as the tangle of invariant manifolds which are points of minima and singularity in the LD plots. As shown by the one dimensional slices of the LD plots, there are multiple such minima and singularities and as the excess energy is increased to positive values, there are regions of discontinuities along the one dimensional slice. Next, as the energy is increased and the bottleneck opens at critical energy Ec, trajectories that leave the potential well and do not return to the surface of section are not observed on the Poincaré section while the LD contour maps clearly identifies these regions as discontinuities in the LD values. These regions lead to escape because they are inside the cylindrical manifolds of the unstable periodic orbit associated with the index-1 saddle equilibrium point [10]. These regions on the isoenergetic two-dimensional surface are also referred to as reactive islands in chemical reaction dynamics [55], [56], [57]. The escape regions or reactive islands that appear over the integration time interval can also be identified by using the forward and backward LD contour maps where these regions appear as discontinuities. In Fig. fig:3 (f), we show these for ΔE=0.125 and τ=50 along with the intersection of the cylindrical manifolds' intersections that are computed using differential correction and numerical continuation. The detailed comparison and extension to high dimensional systems is not the focus of this study and will be discussed in forthcoming work. Thus LD maps also provide a quick and reliable approach for detecting regions that will lead to escape within the observed time, or in the computational context, the integration time.
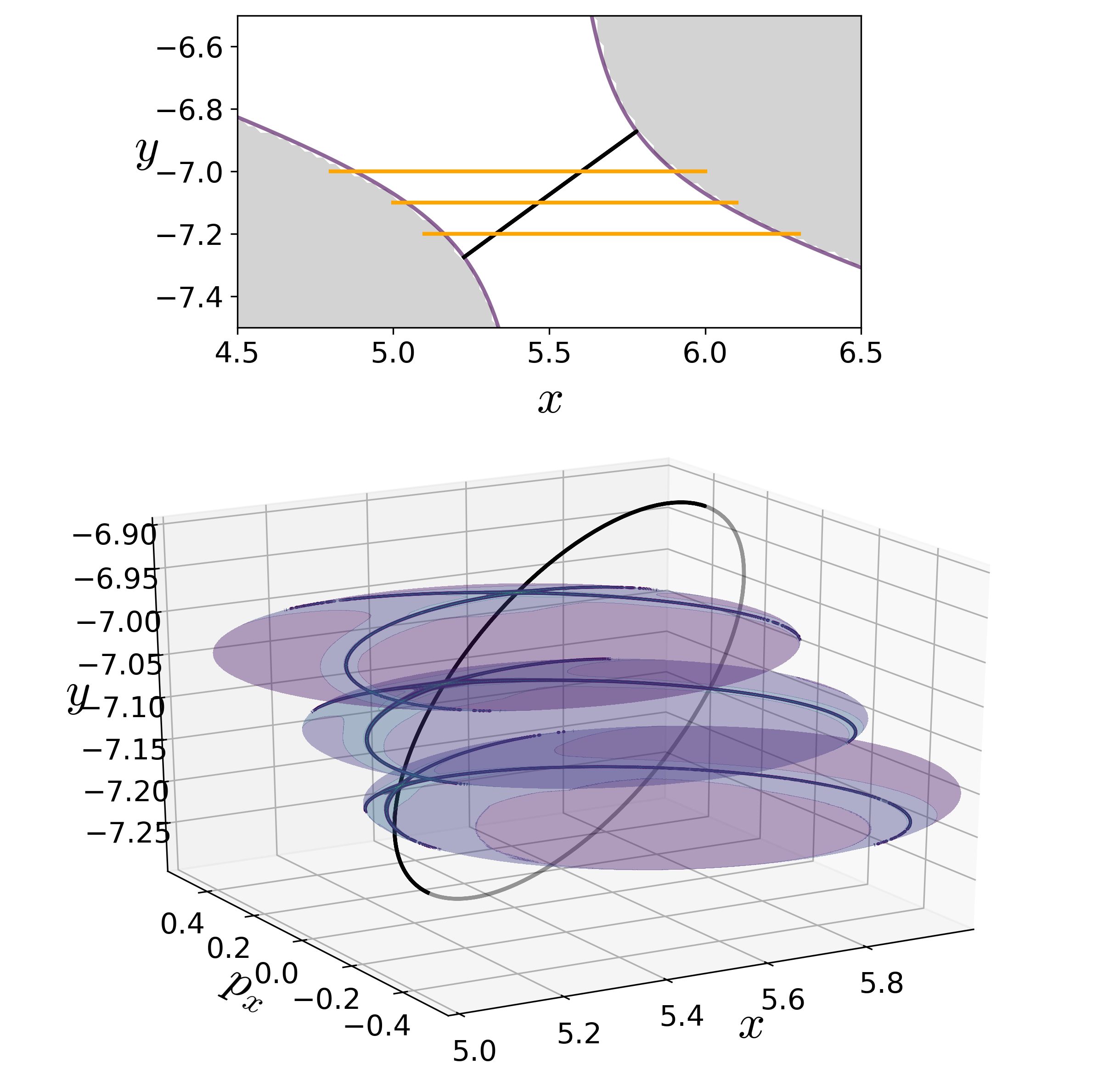
To detect the NHIM in this case, unstable periodic orbit associated with the index-1 saddles (marked by cross in Fig. fig:1 ), we define an isoenergetic two dimensional surface that is parametrized by the y-coordinate and placed near the x-coordinate of the saddle equilibrium that has the negative y-coordinate. This can be expressed as a parametric two dimensional surface
U+xpx(k)={(x,y,px,py)|y=k,py(x,y,px;e)>0}for total energy, e, which is above the critical energy, Ec, k is the y-coordinate. The variable integration time LD contour maps are shown in Fig. fig:4 ) along with the projection of the low dimensional slices (???) in the configuration space and the NHIM. The points on NHIM, which is an unstable periodic orbit for 2 DoF, on this surface is the coordinate with maximum (for variable integration time) LD value. The full visualization of the NHIM as the black ellipse, S1, is in Fig. fig:4 (d) and has been computed using differential correction and numerical continuation (details in App. 5.1 ) and shows clearly that points on this unstable periodic orbit are detected by the LD contour map.
The two dimensional slices represent low dimensional probe of the unstable periodic orbit and the movie of a rotating view can be found here.
Conclusions
In this article, we discussed a trajectory diagnostic method as a low dimensional probe of high dimensional invariant manifolds in 2 DoF nonlinear Hamiltonian systems. This trajectory diagnostic --- Lagrangian descriptor (LD) --- can represent a geometric property of interest in a system with escape/transition and features, that is minima or maxima, in its contour map identify points on the high dimensional invariant manifolds.
Comparing the points on the NHIM in 2 DoF system obtained using the LD method with differential correction and numerical continuation, we also verified the method for a nonlinear autonomous system following our previous work on decoupled and coupled 2 DoF linear system [17]. The LD method based detection of NHIM is simple to implement and quickly provides a lay of the dynamical land which is a preliminirary step in applying phase space transport to problems in physics and chemistry. This method can also be used to set up starting guess for other numerical procedures which rely on good initial guess or can also be used in conjunction with machine learning methods for rendering the smooth pieces of NHIM [45], [58].
References
- T. Komatsuzaki and R. S. Berry, “Dynamical hierarchy in transition states: Why and how does a system climb over the mountain?,” P. Natl. Acad. Sci. USA, vol. 98, no. 14, pp. 7666–7671, 2001.
- T. Komatsuzaki and R. S. Berry, “Regularity in chaotic reaction paths. I. Ar6,” The Journal of Chemical Physics, vol. 110, no. 18, pp. 9160–9173, 1999.
- S. Wiggins, L. Wiesenfeld, C. Jaffé, and T. Uzer, “Impenetrable Barriers in Phase Space,” Phys. Rev. Lett., vol. 86, pp. 5478–5481, 2001.
- C. Jaffé, D. Farrelly, and T. Uzer, “Transition state theory without time-reversal symmetry: chaotic ionization of the hydrogen atom,” Phys. Rev. Lett., vol. 84, pp. 610–613, 2000.
- B. Eckhardt, “Transition state theory for ballistic electrons,” J. Phys. A-Math. Gen., vol. 28, no. 12, p. 3469, 1995.
- P. Collins, G. S. Ezra, and S. Wiggins, “Isomerization dynamics of a buckled nanobeam,” Phys. Rev. E, vol. 86, no. 5, p. 056218, Nov. 2012.
- J. Zhong, L. N. Virgin, and S. D. Ross, “A tube dynamics perspective governing stability transitions: An example based on snap-through buckling,” Int. J. Mech. Sci., vol. 000, no. May, pp. 1–16, 2018.
- L. N. Virgin, “Approximate criterion for capsize based on deterministic dynamics,” Dynamics and Stability of Systems, vol. 4, no. 1, pp. 56–70, 1989.
- J. M. T. Thompson and J. R. de Souza, “Suppression of escape by resonant modal interactions: in shell vibration and heave-roll capsize,” Proc. R. Soc. Lond. A, vol. 452, pp. 2527–2550, 1996.
- S. Naik and S. D. Ross, “Geometry of escaping dynamics in nonlinear ship motion,” Commun. Nonlinear Sci., vol. 47, pp. 48–70, 2017.
- C. Jaffé, S. D. Ross, M. W. Lo, J. E. Marsden, D. Farrelly, and T. Uzer, “Statistical theory of asteroid escape rates,” Physical Review Letters, vol. 89, no. 1, p. 011101, 2002.
- M. Dellnitz et al., “Transport of Mars-crossing asteroids from the quasi-Hilda region,” Physical Review Letters, vol. 94, p. 231102, 2005.
- S. D. Ross, “Statistical theory of interior-exterior transition and collision probabilities for minor bodies in the solar system,” in Libration Point Orbits and Applications, G. Gómez, M. W. Lo, and J. J. Masdemont, Eds. World Scientific, 2003, pp. 637–652.
- H. P. de Oliveira, A. M. Ozorio de Almeida, I. Damião Soares, and E. V. Tonini, “Homoclinic chaos in the dynamics of a general Bianchi type-IX model,” Phys. Rev. D, vol. 65, no. 8, p. 9, 2002.
- S. Patra and S. Keshavamurthy, “Classical-quantum correspondence in a model for conformational dynamics: Connecting phase space reactive islands with rare events sampling,” Chemical Physics Letters, vol. 634, pp. 1–10, Aug. 2015.
- S. Patra and S. Keshavamurthy, “Detecting reactive islands using Lagrangian descriptors and the relevance to transition path sampling,” Physical Chemistry Chemical Physics, vol. 20, no. 7, pp. 4970–4981, 2018.
- S. Naik, Garcı́a-Garrido Vı́ctor J, and S. Wiggins, “Finding NHIM: Identifying High Dimensional Phase Space Structures in Reaction Dynamics using Lagrangian Descriptors,” arXiv preprint arXiv:1903.10264, 2019.
- B. Barbanis, “On the isolating character of the ‘third’ integral in a resonance case,” The Astronomical Journal, vol. 71, p. 415, Aug. 1966.
- P. Brumer and J. W. Duff, “A variational equations approach to the onset of statistical intramolecular energy transfer,” The Journal of Chemical Physics, vol. 65, no. 9, pp. 3566–3574, Nov. 1976.
- M. J. Davis and E. J. Heller, “Semiclassical Gaussian basis set method for molecular vibrational wave functions,” The Journal of Chemical Physics, vol. 71, no. 8, pp. 3383–3395, Oct. 1979.
- E. J. Heller, E. B. Stechel, and M. J. Davis, “Molecular spectra, Fermi resonances, and classical motion,” The Journal of Chemical Physics, vol. 73, no. 10, pp. 4720–4735, Nov. 1980.
- B. A. Waite and W. H. Miller, “Mode specificity in unimolecular reaction dynamics: The Hénon-Heiles potential energy surface,” The Journal of Chemical Physics, vol. 74, no. 7, pp. 3910–3915, Apr. 1981.
- R. Kosloff and S. A. Rice, “Dynamical correlations and chaos in classical Hamiltonian systems,” The Journal of Chemical Physics, vol. 74, no. 3, pp. 1947–1955, Feb. 1981.
- G. Contopoulos and P. Magnenat, “Simple three-dimensional periodic orbits in a galactic-type potential,” Celestial Mechanics, vol. 37, no. 4, pp. 387–414, Dec. 1985.
- M. Founargiotakis, S. C. Farantos, G. Contopoulos, and C. Polymilis, “Periodic orbits, bifurcations, and quantum mechanical eigenfunctions and spectra,” The Journal of Chemical Physics, vol. 91, no. 3, pp. 1389–1402, Aug. 1989.
- B. Barbanis, “Escape regions of a quartic potential,” Celestial Mechanics and Dynamical Astronomy, vol. 48, no. 1, pp. 57–77, 1990.
- D. Babyuk, R. E. Wyatt, and J. H. Frederick, “Hydrodynamic analysis of dynamical tunneling,” The Journal of Chemical Physics, vol. 119, no. 13, pp. 6482–6488, Oct. 2003.
- K. A. Mitchell, J. P. Handley, B. Tighe, J. B. Delos, and S. K. Knudson, “Geometry and topology of escape. I. Epistrophes,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 13, no. 3, pp. 880–891, Sep. 2003.
- K. A. Mitchell, J. P. Handley, J. B. Delos, and S. K. Knudson, “Geometry and topology of escape. II. Homotopic lobe dynamics,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 13, no. 3, pp. 892–902, Sep. 2003.
- K. A. Mitchell, J. P. Handley, B. Tighe, A. Flower, and J. B. Delos, “Chaos-Induced Pulse Trains in the Ionization of Hydrogen,” Physical Review Letters, vol. 92, no. 7, Feb. 2004.
- N. De Leon and B. J. Berne, “Intramolecular rate process: Isomerization dynamics and the transition to chaos,” The Journal of Chemical Physics, vol. 75, no. 7, pp. 3495–3510, Oct. 1981.
- K. A. Mitchell, J. P. Handley, B. Tighe, A. Flower, and J. B. Delos, “Analysis of chaos-induced pulse trains in the ionization of hydrogen,” Physical Review A, vol. 70, no. 4, Oct. 2004.
- K. A. Mitchell and B. Ilan, “Nonlinear enhancement of the fractal structure in the escape dynamics of Bose-Einstein condensates,” Physical Review A, vol. 80, no. 4, Oct. 2009.
- K. A. Mitchell and J. B. Delos, “The structure of ionizing electron trajectories for hydrogen in parallel fields,” Physica D: Nonlinear Phenomena, vol. 229, no. 1, pp. 9–21, May 2007.
- L. Wang, H. F. Yang, X. J. Liu, H. P. Liu, M. S. Zhan, and J. B. Delos, “Photoionization microscopy of the hydrogen atom in parallel electric and magnetic fields,” Physical Review A, vol. 82, no. 2, Aug. 2010.
- F. Balibrea-Iniesta, C. Lopesino, S. Wiggins, and A. M. Mancho, “Lagrangian Descriptors for Stochastic Differential Equations: A Tool for Revealing the Phase Portrait of Stochastic Dynamical Systems,” International Journal of Bifurcation and Chaos, vol. 26, no. 13, p. 1630036, 2016.
- G. T. Craven, A. Junginger, and R. Hernandez, “Lagrangian descriptors of driven chemical reaction manifolds,” Physical Review E, vol. 96, no. 2, p. 022222, 2017.
- A. Junginger and R. Hernandez, “Lagrangian descriptors in dissipative systems,” Physical Chemistry Chemical Physics, vol. 18, no. 44, pp. 30282–30287, 2016.
- A. de la Cámara, A. M. Mancho, K. Ide, E. Serrano, and C. R. Mechoso, “Routes of transport across the Antarctic polar vortex in the southern spring,” J. Atmos. Sci., vol. 69, no. 2, pp. 753–767, 2012.
- C. Mendoza, A. M. Mancho, and S. Wiggins, “Lagrangian descriptors and the assessment of the predictive capacity of oceanic data sets,” Nonlinear Processes in Geophysics, vol. 21, no. 3, pp. 677–689, 2014.
- Garcı́a-Garrido V. J., A. M. Mancho, and S. Wiggins, “A dynamical systems approach to the surface search for debris associated with the disappearance of flight MH370.,” Nonlin. Proc. Geophys., vol. 22, pp. 701–712, 2015.
- C. Lopesino, F. Balibrea-Iniesta, V. J. García-Garrido, S. Wiggins, and A. M. Mancho, “A Theoretical Framework for Lagrangian Descriptors,” International Journal of Bifurcation and Chaos, vol. 27, no. 01, p. 1730001, 2017.
- A. G. Ramos et al., “Lagrangian coherent structure assisted path planning for transoceanic autonomous underwater vehicle missions.,” Scientfic Reports, vol. 4, p. 4575, 2018.
- A. Junginger et al., “Transition state geometry of driven chemical reactions on time-dependent double-well potentials,” Physical Chemistry Chemical Physics, vol. 18, no. 44, pp. 30270–30281, 2016.
- R. Bardakcioglu, A. Junginger, M. Feldmaier, J. Main, and R. Hernandez, “Binary contraction method for the construction of time-dependent dividing surfaces in driven chemical reactions,” Physical Review E, vol. 98, no. 3, Sep. 2018.
- G. S. Ezra and S. Wiggins, “Sampling Phase Space Dividing Surfaces Constructed from Normally Hyperbolic Invariant Manifolds (NHIMs),” The Journal of Physical Chemistry A, vol. 122, no. 42, pp. 8354–8362, 2018.
- G. Contopoulos, “Orbits in Highly Perturbed Dynamical Systems. I. Periodic Orbits,” The Astronomical Journal, vol. 75, p. 96, Feb. 1970.
- E. J. Heller, E. B. Stechel, and M. J. Davis, “Molecular spectra, Fermi resonances, and classical motion,” The Journal of Chemical Physics, vol. 73, no. 10, pp. 4720–4735, 1980.
- M. J. Davis and E. J. Heller, “Quantum dynamical tunneling in bound states,” The Journal of Chemical Physics, vol. 75, no. 1, pp. 246–254, Jul. 1981.
- C. C. Martens and G. S. Ezra, “Classical and semiclassical mechanics of strongly resonant systems: A Fourier transform approach,” The Journal of Chemical Physics, vol. 86, no. 1, pp. 279–307, 1987.
- S. Wiggins, “The role of normally hyperbolic invariant manifolds (NHIMS) in the context of the phase space setting for chemical reaction dynamics,” Regular and Chaotic Dynamics, vol. 21, no. 6, pp. 621–638, Nov. 2016.
- J. A. J. Madrid and A. M. Mancho, “Distinguished trajectories in time dependent vector fields,” Chaos, vol. 19, p. 013111, 2009.
- A. S. Demian and S. Wiggins, “Detection of Periodic Orbits in Hamiltonian Systems Using Lagrangian Descriptors,” International Journal of Bifurcation and Chaos, vol. 27, no. 14, p. 1750225, 2017.
- V. J. García-Garrido, J. Curbelo, A. M. Mancho, S. Wiggins, and C. R. Mechoso, “The Application of Lagrangian Descriptors to 3D Vector Fields,” Regular and Chaotic Dynamics, vol. 23, no. 5, pp. 551–568, Sep. 2018.
- N. De Leon, “Cylindrical manifolds and reactive island kinetic theory in the time domain,” J. Chem. Phys., vol. 96, pp. 285–297, 1992.
- N. De Leon, M. A. Mehta, and R. Q. Topper, “Cylindrical manifolds in phase space as mediators of chemical reaction dynamics and kinetics. I. Theory,” J. Chem. Phys., vol. 94, pp. 8310–8328, 1991.
- N. De Leon, M. A. Mehta, and R. Q. Topper, “Cylindrical manifolds in phase space as mediators of chemical reaction dynamics and kinetics. II. Numerical considerations and applications to models with two degrees of freedom,” J. Chem. Phys., vol. 94, pp. 8329–8341, 1991.
- M. Feldmaier et al., “Invariant Manifolds and Rate Constants in Driven Chemical Reactions,” The Journal of Physical Chemistry B, vol. 123, no. 9, pp. 2070–2086, Mar. 2019.